Mathematics: Running fixes

The sum of angles in a triangle is 180°

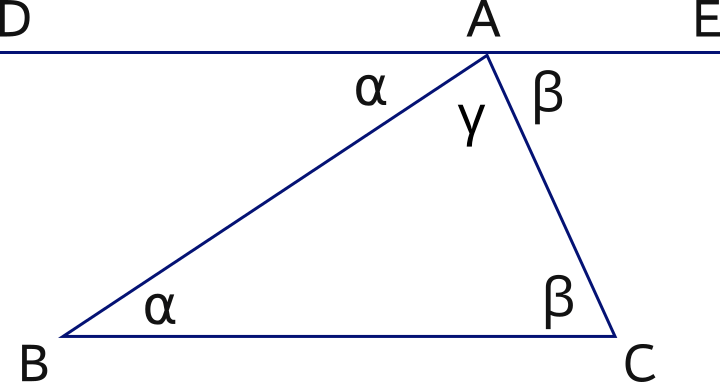
Draw a triangle ABC, then draw a line DAE parallel to line BC. Now, angles α and β in the triangle equal angles DAB and EAC, respectively. Therefore, the sum of angles in the triangle is 180° : a straight line.

“Doubling the angle” yields two equal angles

α = 30° , β = 60°
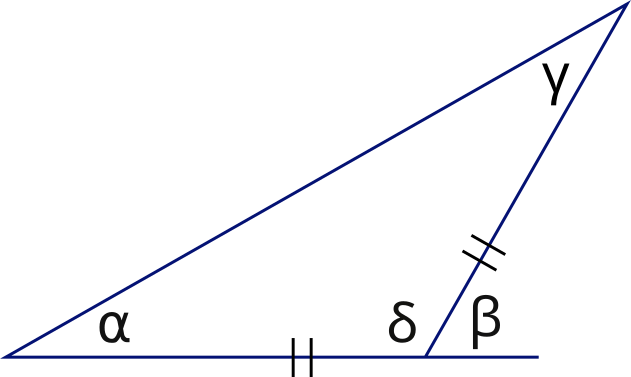
thus γ = 30°

So, α + δ + γ = 180°
α + 180 - β + γ = 180°
2α = β
α + 180 - 2α + γ = 180°
180° - α + γ = 180°
-α + γ = 0
γ = α

Two equal angles render an triangle isosceles

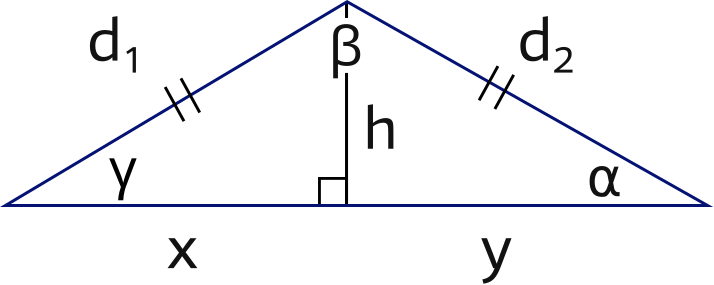
isosceles triangle if two angles are equal

In the triangle on the right, α = γ and β = 2α.
By constructing the bisector h of angle β we create two little triangles in which x=y.
Therefore, d₁=d₂.

Next math chapter: Distance of horizon

Further reading:
Online navigation courses.
Flotilla sailing holidays.
RYA & ASA sailing schools in Greece.
Yacht charters guide.

Site map | A-Z index | Register