Mathematics: Sextant angles

Vertical sextant angle

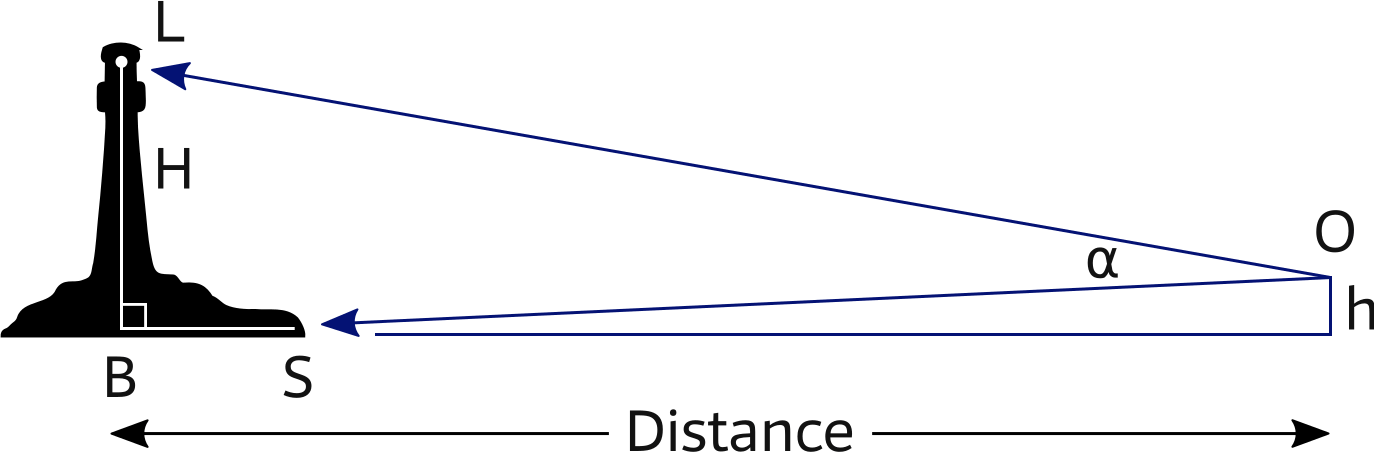
The triangle OBL can be described in terms of H, α and Distance:

Distance = H / tan(α)

where, the angle is in radians (0—2π) and both height and distance are in metres.

• The relations between radians and degrees is:
  α = A × π / 180
  with “A” being the same angle in degrees.
• To describe angle A in minutes total, then A × 60 = a, thus α = (a / 60) × (π / 180). So, α = a / 3438, “a” being the angle in arc minutes.
• Fact: tan(x) = x, if angle x is small.

Resulting in (with π = 3.14): Distance (m)= H × 3438 / a

• Furthermore, distance in Nautical Miles = distance in meters / 1852.

Voilà, a very practical equation:
Distance = 1.856 × H / a
It contains just two approximations, both of neglitible influence. First, we left out the tan function and second we used 3.14 for π.

Please realize that a smaller angle improves the approximation of the tan. Yet, as an opposing effect the instrument error of a smaller sextant angle increases.

All in all, the factor 1.856 is not a typo, and just by chance near to the nautical mile: 1.852 kilometres. If you are still reading, you are very brave person and might agree that it originates from (60 × 180) / (π × 1852).

So far we considered a perfect triangle (OBL) and forgot that life isn't always perfect. Height h is usually quite small, but distance SB sometimes is not. This leads to an extra premise, which is seldom mentioned by other navigation textbooks:
Angle OLS should be bigger than 15°.

Further reading:
Without tides the Mediterranean is the perfect cruising venue with RYA & ASA sailing schools out of Athens into the Saronic or Cyclades (Santorini, Paros, Mykonos,…) and in the Ionian: Lefkas,
or back to chapter 5 of the navigation course,
or learn to sail bareboat with a private RYA ASA instructor.